Show that $K = \dfrac{\overrightarrow p \cdot \overrightarrow p}{2m}$.
Solution
$$K=\dfrac{1}{2}mv^2\text{... multiply by}\dfrac{m}{m}$$
$$K=\dfrac{1}{2m}m^2v^2\implies K=\dfrac{m^2v^2}{2m}\implies K=\dfrac{(mv)^2}{2m}$$
However, we know that mv is |P⃗|
$$K=\dfrac{(mv)^2}{2m}\implies K=\dfrac{|\overrightarrow{P}|^2}{2m}$$
The square of the magnitude of a vector is the dot product of the vector by itself.
$$K=\dfrac{|\overrightarrow{P}|^2}{2m}=\dfrac{\overrightarrow{P}\cdot\overrightarrow{P}}{2m}$$
What is the change in momentum of a 3.0-kg ball moving at 3.0 m/s perpendicular to a wall rebounding from the wall at 1.75 m/s?
Solution
ΔP = Pf − Pi = mvf − mvi = m(vf − vi)
ΔP = 3.0kg(1.75m/s − 3.0m/s)
ΔP = − 3.75kgm/s
The negative sign indicates that the linear momentum has decreased. What is the momentum (as a function of time) of a 5.0-kg particle moving with a velocity $v(t)=(3\hat{i}+\dfrac{4t}{s}\hat{j})m/s$? What is the net force acting on this particle?
P⃗ = mv⃗ ⟹ P⃗(t) = mv⃗(t)
$$\overrightarrow{P}(t)=5.0kg((3\hat{i}+\dfrac{4t}{s}\hat{j})m/s)$$
$$\overrightarrow{P}(t)=(15\hat{i}+\dfrac{12t}{s}\hat{j})kgm/s)$$
A man is marooned at rest on level frictionless ice. In desperation, he hurls his shoe to the right at 20 m/s. If the man weighs 740 N and the shoe weighs 6.0 N, what is the speed with which the mans leaves to the left?
Solution
First, we need to calculate the masses of the man & the shoe. Assuming the acceleration due to gravity to be 10m/s2, the masses would be 74kg, and 0.6kg. To solve the problems, we must make use of the idea of the Law of Conservation of Linear Momentum.
ΔP⃗ = 0
P⃗i = P⃗f
0 = (74kg)v1f + (0.6kg)(20m/s)
$$v_{1f}=-\dfrac{162}{37}m/s$$
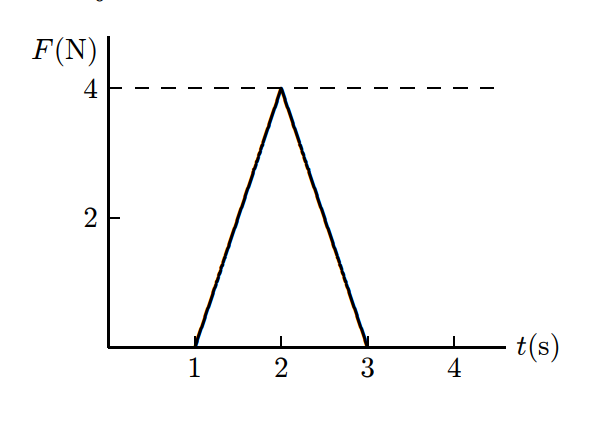
The negative sign indicates that the velocity of the man has a direction opposite to that of the shoe’s A 5-kg object can move along the x axis. It is subjected to a force F⃗ in the positive x direction; a graph of F as a function of time t is shown below. Over the time the force is applied, what is the change in the velocity of the object?

Solution
To calculate the change in velocity, we need to first find the impulse and from the impulse, we can find the change in linear momentum which will give us the change in velocity.
J⃗ = ΔP⃗ = mΔv⃗
The impulse is the important thing to calculate here. We know that the impulse is given by J⃗ = ∫titfF⃗(t)dt. However, since the force function here has a relatively easy shape (triangle), calculating the area would be a very easier job to do.
$$|\overrightarrow{J}|=\dfrac{1}{2}(3s-1s)(4N)$$
|J⃗| = 4Ns
Since we have found the the impulse now, it means we have found the change in linear momentum, which is 4Ns.
$$J=m\Delta v\implies \Delta v=\dfrac{J}{m}$$
$$\Delta v= \dfrac{4Ns}{5kg}$$
Δv = 0.8m/s