
The Atom
AZX→ A indicates the mass number while Z indicates the atomic number. Example: 42He
We usually use the unit amu when discussing the masses of atoms and molecules. $1 \text{ amu} = \dfrac{1}{2} \text{mass of Carbon-12}$. It is approximately equal to the average of the rest masses of a proton and a neutron.
We model atoms as spherical balls in space and we estimate the radii as follow: $R=R_0A^{\frac{1}{3}}$ while R0 is average size of the nucleus 1.2 × 10 − 15m
An element has a unique atomic number and its mass number might differ.

Rutherford Atomic Model Rutherford’s Gold Foil Experiment:
Alpha particles directed at gold foil
Most passed through, some deflected
Conclusion: Small, dense, positively charged nucleus
Limitations:
Could not explain stability of atoms
Could not explain discrete spectral lines of elements
Bohr Atomic Model Improvements on Rutherford’s Model:
Introduced quantized energy levels
Electrons orbit nucleus in specific orbits
Energy emitted/absorbed when electrons jump between orbits
Key Postulates:
Electrons move in fixed orbits without radiating energy
Energy of orbits: $E_n = -\frac{13.6 \text{ eV}}{n^2}$ (for hydrogen atom)
Mass Defect of an Atom Concept: The difference between the mass of an atom and the sum of the masses of its constituent protons, neutrons, and electrons.
Mass defect: Δm = Zmp + Nmn + Zme − matom
Indicates the binding energy of the nucleus
Example: Mass Defect Calculation Given the following data, calculate the mass defect of a carbon-12 atom:
Mass of carbon-12 atom = 12 u
Mass of a proton = 1.007276 u
Mass of a neutron = 1.008665 u
Mass of an electron = 0.000548 u
$$\begin{aligned}
\text{Number of protons} &= 6 \\
\text{Number of neutrons} &= 6 \\
\text{Number of electrons} &= 6 \\
\text{Total mass of protons} &= 6 \times 1.007276 \text{ u} = 6.043656 \text{ u} \\
\text{Total mass of neutrons} &= 6 \times 1.008665 \text{ u} = 6.05199 \text{ u} \\
\text{Total mass of electrons} &= 6 \times 0.000548 \text{ u} = 0.003288 \text{ u} \\
\text{Total mass of constituents} &= 6.043656 \text{ u} + 6.05199 \text{ u} + 0.003288 \text{ u} = 12.098934 \text{ u} \\
\text{Mass defect} &= 12.098934 \text{ u} - 12 \text{ u} = 0.098934 \text{ u}
\end{aligned}$$
Binding Energy Concept: Energy required to disassemble a nucleus into its constituent protons and neutrons.
Calculated using mass defect: Δm = Zmp + Nmn − mnucleus
Binding energy: Eb = Δmc2
Binding energy per nucleon can be found using $E_bN = \dfrac{E_b}{A}$
Binding energy per nucleon indicates stability of the nucleus
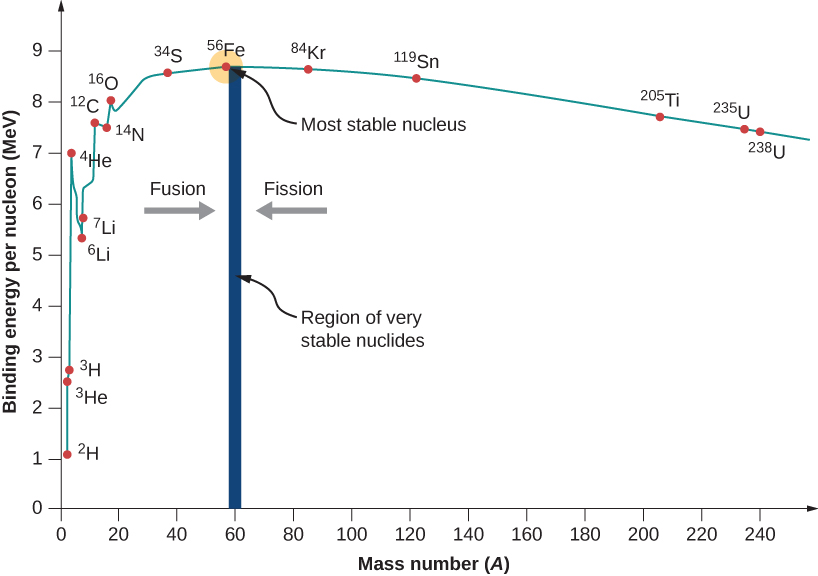
Example: Binding Energy Calculation Calculate the binding energy per nucleon for a helium-4 nucleus (mass = 4.002603 u).
$$\begin{aligned}
\text{Mass of 2 protons} &= 2 \times 1.007825 \text{ u} = 2.01565 \text{ u} \\
\text{Mass of 2 neutrons} &= 2 \times 1.008665 \text{ u} = 2.01733 \text{ u} \\
\text{Total mass of nucleons} &= 2.01565 \text{ u} + 2.01733 \text{ u} = 4.03298 \text{ u} \\
\text{Mass defect} &= 4.03298 \text{ u} - 4.002603 \text{ u} = 0.030377 \text{ u} \\
\text{Binding energy} &= 0.030377 \text{ u} \times 931.5 \text{ MeV/u} = 28.299 \text{ MeV} \\
\text{Binding energy per nucleon} &= \frac{28.299 \text{ MeV}}{4} = 7.07475 \text{ MeV/nucleon}
\end{aligned}$$
Half-Life of Radioactive Materials Concept: The half-life of a radioactive isotope is the time it takes for half of the radioactive atoms to decay.
Exponential decay: N(t) = N0e − λt
Relationship between half-life and decay constant: $T_{1/2} = \frac{\ln 2}{\lambda}$
Activity: A = λN
Example on half life Calculate the age of the Shroud of Turin given that the amount of 14C found in it is 92% of that in living tissue.
$$\dfrac{N}{N_0} = e^{-\lambda t}.$$
0.92 = e − λt
ln 0.92 = − λt ⟹ − 0.0834 = − λt.
We can find the λ using one important fact and that is $\lambda = \frac{0.693}{t_{1/2}}$. We know the half life of Carbon and that is about 5730 years. So, t can be found
$$t = \dfrac{0.0834}{\frac{0.693}{5730 \, y}} = 690 \, y.$$
Another example A sample of a radioactive isotope has a half-life of 8 hours. If the initial activity of the sample is 1600 Bq, what will be the activity after 24 hours?
$$A(t) = A_0 \left( \frac{1}{2} \right)^{t/T_{1/2}} = 1600 \left( \frac{1}{2} \right)^{24/8} = 1600 \left( \frac{1}{2} \right)^3 = 1600 \times \frac{1}{8} = 200 \text{ Bq}$$
Types of Radiation Alpha Radiation:
Helium nuclei (2 protons, 2 neutrons)
Low penetration, can be stopped by paper
Beta Radiation:
Electrons (beta-minus) or positrons (beta-plus)
Moderate penetration, can be stopped by aluminum
Gamma Radiation:
High-energy electromagnetic radiation
High penetration, can be stopped by thick lead or concrete
Conservation Laws in Radioactive Decay Key Conservation Laws:
Conservation of mass-energy: Total mass and energy remain constant
Conservation of charge: Total charge remains constant
Conservation of momentum: Total momentum remains constant
Conservation of nucleon number: Total number of protons and neutrons remains constant
Applications of Research Reactors Medicine:
Production of medical isotopes (e.g., Technetium-99m for diagnostic imaging)
Treatment of cancer using neutron therapy
Industry:
Neutron activation analysis for material composition
Isotopes for radiography to inspect welding joints and structural integrity
Research:
Study of neutron scattering to understand material properties
Development of new materials and nuclear technologies
Nuclear Energy Concept: Nuclear fission and chain reactions.
Fission: Splitting of a heavy nucleus into lighter nuclei, releasing energy
Chain reaction: Neutrons produced in fission cause further fission reactions
Application: Nuclear power plants generate electricity using controlled fission reactions
Example: Nuclear Fission Example: Fission of Uranium-235
$$^{235}_{92}\text{U} + ^1_0\text{n} \rightarrow ^{141}_{56}\text{Ba} + ^{92}_{36}\text{Kr} + 3 ^1_0\text{n} + \text{energy}$$
Each fission event releases approximately 200 MeV of energy
Energy used to produce steam and drive turbines for electricity generation
Neutron Activation Analysis (NAA) Concept: Irradiation of a sample with neutrons.
Formation of radioactive isotopes
Emission of characteristic gamma rays
Determination of composition and concentration of elements
Example: Application in Archaeology Analysis of ancient pottery to determine composition and origin, providing insights into trade routes and cultural exchanges.
Sample is irradiated in a research reactor
Induced radioactivity measured and analyzed
Elemental composition deduced from gamma-ray spectra
Beta-minus Decay of Carbon-14 Carbon-14 (14C) undergoes beta-minus decay. Write the balanced nuclear equation for this decay process and identify the resulting daughter nucleus.
$$^{14}_{6} \text{C} \rightarrow ^{14}_{7} \text{N} + \beta^- + \bar{\nu}_e$$
The daughter nucleus is Nitrogen-14 (714N).
Beta-plus Decay of Potassium-40 Potassium-40 (40K) can undergo beta-plus decay. Write the balanced nuclear equation for this decay process and identify the resulting daughter nucleus.
$$^{40}_{19} \text{K} \rightarrow ^{40}_{18} \text{Ar} + \beta^+ + \nu_e$$
The daughter nucleus is Argon-40 (1840Ar).
Beta-minus Decay of Strontium-90 Strontium-90 (90Sr) undergoes beta-minus decay. Write the balanced nuclear equation for this decay process and identify the resulting daughter nucleus.
$$^{90}_{38} \text{Sr} \rightarrow ^{90}_{39} \text{Y} + \beta^- + \bar{\nu}_e$$
The daughter nucleus is Yttrium-90 (3990Y).
Beta-plus Decay of Fluorine-18 Fluorine-18 (18F) undergoes beta-plus decay. Write the balanced nuclear equation for this decay process and identify the resulting daughter nucleus.
$$^{18}_{9} \text{F} \rightarrow ^{18}_{8} \text{O} + \beta^+ + \nu_e$$
The daughter nucleus is Oxygen-18 (818O).
Beta-minus Decay of Phosphorus-32 Phosphorus-32 (32P) undergoes beta-minus decay. Write the balanced nuclear equation for this decay process and identify the resulting daughter nucleus.
$$^{32}_{15} \text{P} \rightarrow ^{32}_{16} \text{S} + \beta^- + \bar{\nu}_e$$
The daughter nucleus is Sulfur-32 (1632S).
Beta-minus Decay of Iodine-131 Iodine-131 (131I) undergoes beta-minus decay. Write the balanced nuclear equation for this decay process and identify the resulting daughter nucleus.
$$^{131}_{53} \text{I} \rightarrow ^{131}_{54} \text{Xe} + \beta^- + \bar{\nu}_e$$
The daughter nucleus is Xenon-131 (54131Xe).
Beta-plus Decay of Sodium-22 Sodium-22 (22Na) undergoes beta-plus decay. Write the balanced nuclear equation for this decay process and identify the resulting daughter nucleus.
$$^{22}_{11} \text{Na} \rightarrow ^{22}_{10} \text{Ne} + \beta^+ + \nu_e$$
The daughter nucleus is Neon-22 (1022Ne).
Beta-minus Decay of Technetium-99 Technetium-99 (99Tc) undergoes beta-minus decay. Write the balanced nuclear equation for this decay process and identify the resulting daughter nucleus.
$$^{99}_{43} \text{Tc} \rightarrow ^{99}_{44} \text{Ru} + \beta^- + \bar{\nu}_e$$
The daughter nucleus is Ruthenium-99 (4499Ru).
Beta-minus Decay of Cesium-137 Cesium-137 (137Cs) undergoes beta-minus decay. Write the balanced nuclear equation for this decay process and identify the resulting daughter nucleus.
$$^{137}_{55} \text{Cs} \rightarrow ^{137}_{56} \text{Ba} + \beta^- + \bar{\nu}_e$$
The daughter nucleus is Barium-137 (56137Ba).
Beta-minus Decay of Thallium-204 Thallium-204 (204Tl) undergoes beta-minus decay. Write the balanced nuclear equation for this decay process and identify the resulting daughter nucleus.
$$^{204}_{81} \text{Tl} \rightarrow ^{204}_{82} \text{Pb} + \beta^- + \bar{\nu}_e$$
The daughter nucleus is Lead-204 (82204Pb).