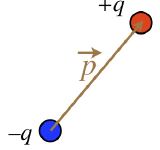
Consider two equal point charges, one positive, and the other negative, that are held rigidly at a fixed separation distance (if you like, you can imagine a tiny rigid rod holding them at fixed relative positions). We have already seen what the field of such a dipole configuration looks like earlier. We could forever treat such a configuration as a combination of two point particles, but it is helpful to package them so that we can treat them as a single entity and not have to go back and recalculate things. To that end, we define a vector quantity known as an electric dipole moment as follows:
|p⃗| ≡ q d

The magnitude of the dipole moment is defined as the product of the absolute value of one of the two charges, multiplied by the distance separating the two charges. Conventionally, the direction of the dipole moment is that it points from the negative charge to the positive charge.
We consider now the effect that a uniform electric field has on a dipole. Note that while we will be assuming a uniform field, in reality we mean that the amount that the external field changes across the length of the dipole is negligible. Also, as will generally be the case going forward, when we draw a diagram of a uniform field, we will represent it with a set of parallel field lines.
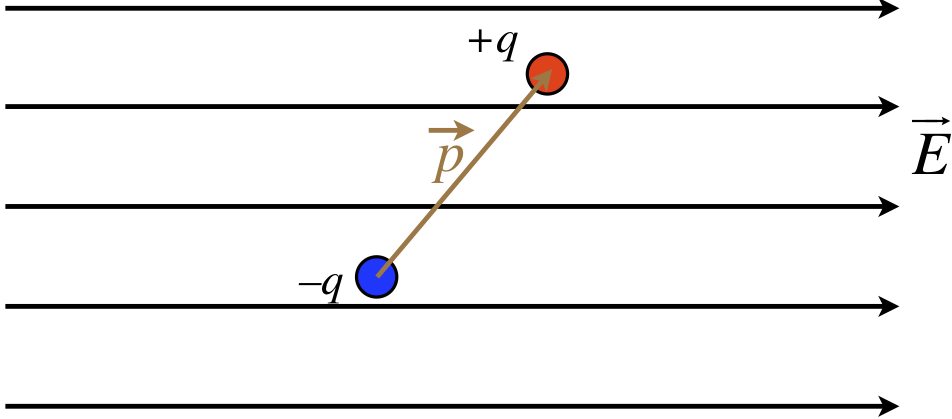
We begin by considering the force on the dipole. Certainly each individual charge feels a new force from the field, but the charges are equal in magnitude, and the forces act in opposite directions, so the net force on it is zero. With no net force, the center of mass of the dipole will not accelerate, but there will clearly be a torque exerted on this object. We can introduce a coordinate system above, and determine what this torque is, in terms of the field and dipole moment.
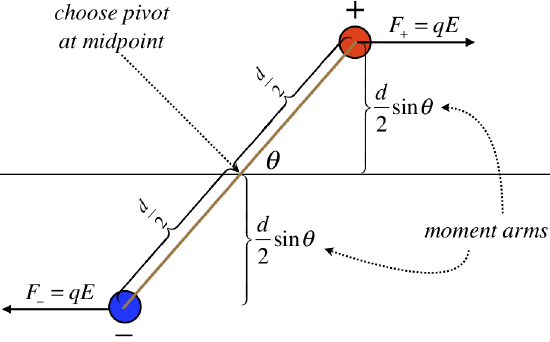
Multiplying the forces by the moment arms, and summing, we find that the magnitude of the torque on this dipole is:
$$\tau = 2\left[ qE\frac{d}{2}\sin\theta\right] = qd\;E\;\sin\theta$$
The magnitude of the dipole moment appears in the equation, as does the strength of the electric field, and the sine of the angle between them. This would suggest a connection to the cross product of the dipole moment and the electric field vector. Looking at the diagram, we see that the torque will cause clockwise rotational acceleration, which means that the torque vector points into the page. Indeed, the right-hand-rule applied to the cross product of p⃗ and E⃗ results in a vector that points into the page, so we conclude:
τ⃗ = p⃗ × E⃗
Suppose we release the dipole in the diagram above from rest. Clearly it will begin to rotate, which means it will gain kinetic energy. This energy must come from somewhere, and in fact it comes from the work done by the electric field. But the electric field exerts a conservative force, so we can also express it in terms of a potential energy. The change in potential energy due to a conservative force is the negative of the work done by that force. So let’s consider the work done by the electric force on the charges of the dipole as the dipole rotates (note, there is no net force on the dipole as a whole, so the movement of its center of mass doesn’t change the potential energy).
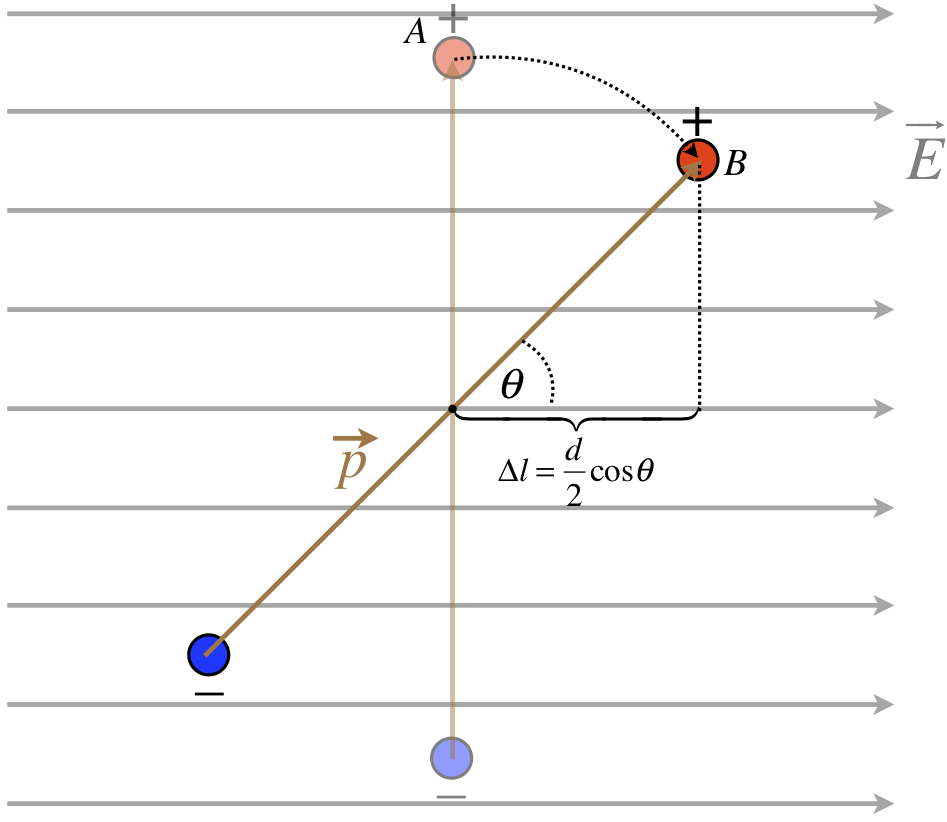
Only the displacement of each charge along the direction of the force (which is parallel to the electric field) counts toward the work done. The force on each charge has a magnitude of qE, and the force acts in the direction of the displacement for both charges (remember the force on the negative charge is the opposite direction of the field), which makes the work done positive, and the change in potential energy negative. For both charges charge we therefore have:
$$\Delta U_{dipole} = -2W\left(A\rightarrow B\right) = -2F\Delta l = -2\left(qE\right)\left(\frac{d}{2}\cos\theta\right) = -\left(qd\right)E\cos\theta$$
While the torque evoked the idea of a cross product, the potential energy screams out dot product. If we follow a typical convention and define the zero potential energy exist in the configuration when the dipole is perpendicular to the field, then we have:
Udipole = − p⃗ ⋅ E⃗
Advanced
Show that the electric filed by a dipole along its axis is given by
$$\overrightarrow E = 2k\dfrac{p}{r^3} \widehat i$$
Hint: For this calculation, place both charges on the x-axis, equal distances from the origin, with the positive charge on the positive side of the origin.